EBOB ve EKOK Hesaplama Nasıl Yapılır?
İki sayının en büyük ortak bölenini ve en küçük ortak katını hesaplama yöntemini milattan önce 300’lü yıllarda Öklid, ‘Elementler’ isimli …

İki sayının en büyük ortak bölenini ve en küçük ortak katını hesaplama yöntemini milattan önce 300’lü yıllarda Öklid, ‘Elementler’ isimli eserinde paylaşmıştır. Bu yönteme ‘Öklit Algoritması’ deniyor fakat buradan türetilmiş daha kolay hesaplama yöntemleri de mevcut.
Genellikle sayıları asal çarpanlarına ayırıp, ardından duruma göre uygun çarpanları seçerek istersek EBOB’u ya da EKOK’u hesaplayabiliyoruz. Gerçek dünya’da bir işe yaramayacaklarmış gibi gözükse de, tekstil gibi pek çok farklı sektörde kullanılabiliyor. Gelin şimdi EBOB ve EKOK nedir, nasıl hesaplanır birlikte bakalım.

EBOB Nedir?
En büyük ortak bölen, iki veya daha fazla sayının en büyük ortak bölenini ifade eder. Hesaplamak için kullanılabilecek iki popüler metot vardır. Bir tanesi Öklidin Elementler’de ifade ettiği Öklid algoritması, ikincisi ise kısmen daha kolay ve daha sık kullanılan bir metot.
Herhangi iki sayının EBOB’unu ‘EBOB()’ şeklinde gösterelim. Öklid algoritması herhangi iki sayı üzerinde çalışan bir algoritmadır. Elinizde a ve b sayıları varken üç durumdan söz edebiliriz.
- 1. Durum: a ve b sayısı birbirine eşittir (a=b)
- 2. Durum: a sayısı b sayısından büyüktür (a>b)
- 3. Durum: b sayısı a sayısından büyüktür (b>a)
Eşitlik durumunda, iki sayı eşit olduğundan en büyük ortak bölenleri kendileridir. Yani EBOB(a,b)=a=b olur.
Diğer herhangi bir durumda büyük olan sayıyı küçük olana böler, kalan değer sıfır olana dek küçük sayı ile bölmeye devam ederiz. Şimdi a, b’den büyükken eğer a ile b nin bölümünden kalan c ve c sıfırdan farklı ise, bu sefer b ile c yi bölüyoruz ve kalanına bakıyoruz. Eğer sıfır değilse c ile bu sayıyı bölerek işlemlere devam ediyoruz. Kalan 0 olduğu zaman bulduğumuz küçük bölen, başlangıçtaki iki sayının EBOB’u oluyor.
EBOB nasıl hesaplanır?
- Yöntem #1: Öklit algoritması ile hesaplama
- Yöntem #2: Çarpanlarına ayırarak hesaplama
Yöntem #1: Öklit algoritması ile hesaplama:
- Adım 1#: Bölerek başlama
- Adım 2#: 0’a ulaşana kadar bölme işlemi
Bir örnek üzerinden ilerleyelim. Sayılarımız 28 ve 16 olsun.
Adım 1#: Bölerek başlama

28 ile 16’yı böldüğümüzde kalan 12 oluyor, sıfırdan farklı olduğu için devam ediyoruz
Adım 2#: 0’a ulaşana kadar bölmeye devam etmek

16 ile 12’yi böldüğümüzde kalan sayı 4 oluyor halen sıfırdan büyük olduğu için devam ediyoruz. Son aşamada ise elimizdeki sayı 12 ve 4 oluyor. Bunların bölümünde ise elimizde kalan 0 oluyor. Bu durumda 4 sayısı 28 ve 16’nın EBOB’u oluyor. Yani EBOB (28, 16)=4
Yöntem #2: Çarpanlarına ayırarak hesaplama:
- Adım 1#: Asal çarpanlarına ayırmak
- Adım 2#: Ortak olan asal çarpanları seçmek
Adım 1#: Asal çarpanlarına ayırmak
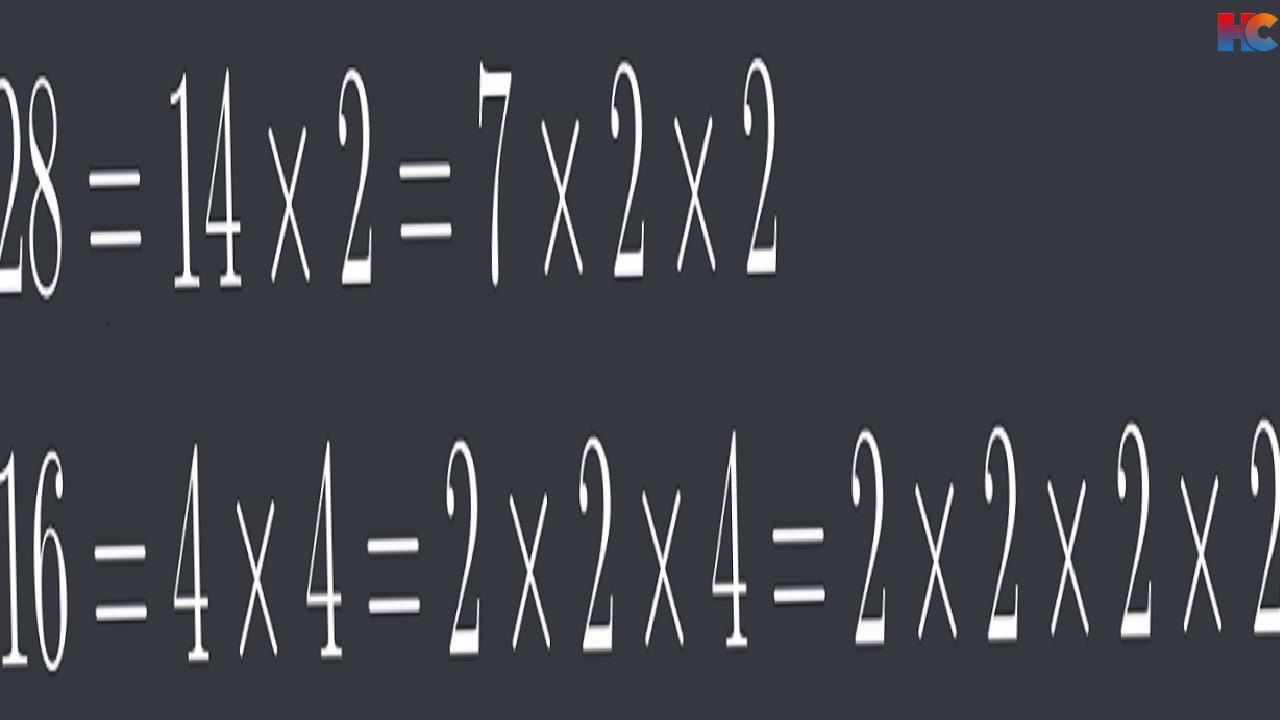
Elimizdeki sayıar 28 ve 16’yı ilk olarak asal çarpanlarına ayıralım.
Adım 2#: Ortak olan asal çarpanları seçmek ve bulunan ortak sayıları çarpmak

Şimdi ortak olan asal çarpanları seçelim, iki sayıda da 2 adet 2’nin ortak olduğunu görüyoruz. Bu sayıları çarparak en büyük ortak bölenlerini elde etmiş oluruz. Tabii ki cevap yine 4 olur.
Peki EKOK nedir?

En küçük ortak kat, verilen iki veya daha fazla sayının en küçük ortak katını bulmamıza olanak sağlıyor. Hesaplamada yine asal çarpanlardan yararlanabileceğimiz gibi, iki sayının en büyük ortak bölenini kullanarak da EKOK hesaplayabiliyoruz.
Birinci metotta asal çarpanları sıralayarak başlıyoruz. Ardından ortak çarpanları birer defa yazıp, ortak olmayanları da dahil ederek çarpma yapıyoruz ve sonuca ulaşıyoruz. İkinci metotta ise elimizdeki iki sayıyı çarpıp mutlak değer içerisine alıyoruz. Ardından sonucu bu iki sayının EBOB’una bölerek EKOK’a ulaşmış oluyoruz. Şimdi bunlara detaylıca bakalım.
EKOK nasıl hesaplanır?
- Yöntem #1: Asal çarpanları kullanarak EKOK hesaplama
- Yöntem #2: Asal çarpanları üslerle ifade ederek EKOK hesaplama
Yöntem #1: Asal çarpanları kullanarak EKOK hesaplama:
- Adım 1#: 28 ve 16’yı asal çarpanlarına ayırma
- Adım 2#: Aynı olan çarpanlardan birer tane almak ve sonuca ulaşma
Adım 1#: 28 ve 16’yı Asal çarpanlarına ayırma
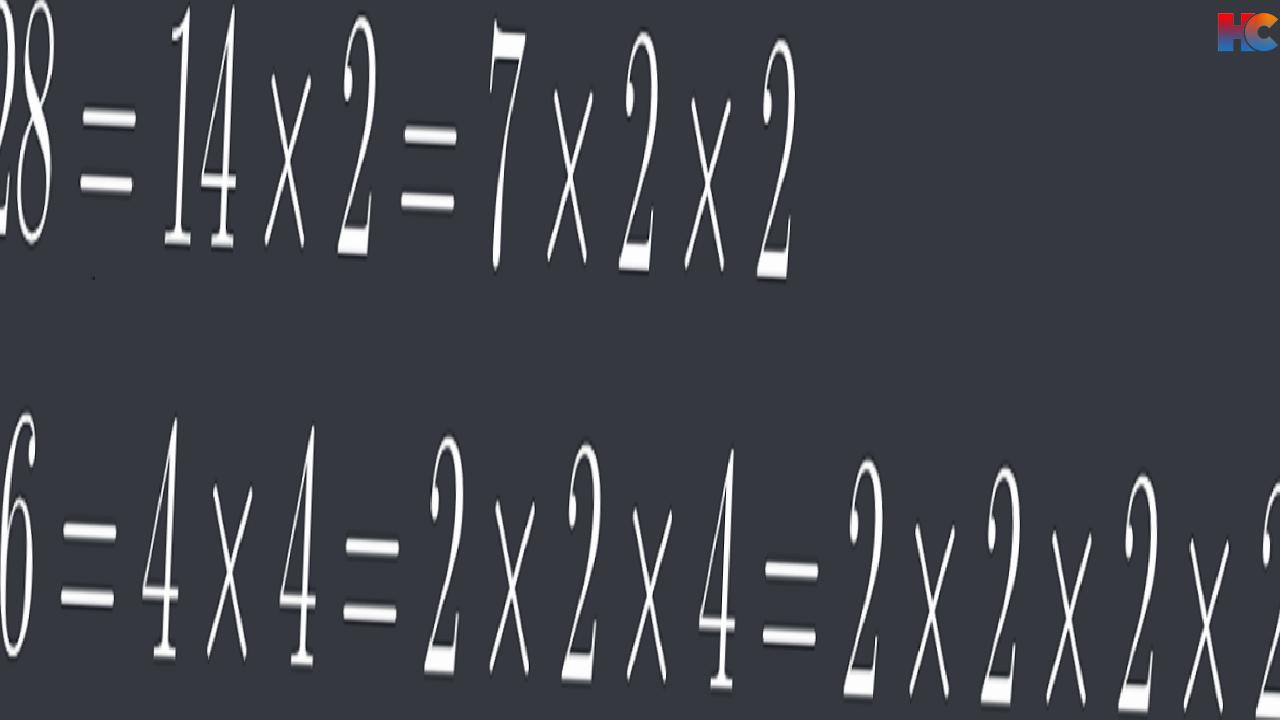
EBOB anlatımında yapıldığı gibi aynı şekilde 28 ve 16’yı asal çarpanlarına ayırıyoruz
Adım 2#: Aynı olan çarpanlardan birer tane almak ve sonuca ulaşmak

Şimdi aynı olan çarpanlardan birer tanesini alacağız, siyah işaretli ikiler her iki sayının da çarpanı olduğundan birer defa alınacaklar. Bunlar dışındaki çarpanlar da direkt olarak eklenecek. Bu durumda EKOK (28, 16)=7x2x2x2x2=112 olarak hesaplanıyor.
Bu metotta dikkat etmemiz gereken nokta ortak asal çarpanlardan yalnızca birer tanesini çarpmaya ekliyor olmamız. Siyah daire içindeki 2’lerden her iki sayının çarpanlarında da olduğu için onlardan birer tanesini işleme ekliyoruz. Böylelikle 4 adet 2 ve bir adet 7 yi çarparak sonuca ulaşabiliyoruz.
Yöntem #2: Asal çarpanları üslerle ifade ederek EKOK hesaplama:
- Adım 1#: Asal çarpanları belirlemek
- Adım 2#: Belirlenen sayıları üslü sayılar halinde düzenlemek
- Adım 3#: Kuvveti en yüksek olanlar ile çarpmak
Bu metot bir önceki metodun daha kolay bir versiyonu. Bu sefer sayıları asal çarpanlarına ayırdıktan sonra üslü sayılar haline gelecek şekilde düzenleme yapıyoruz. Yukarıdaki örnekten devam edecek olursak:
Adım 1#: Asal çarpanları belirlemek
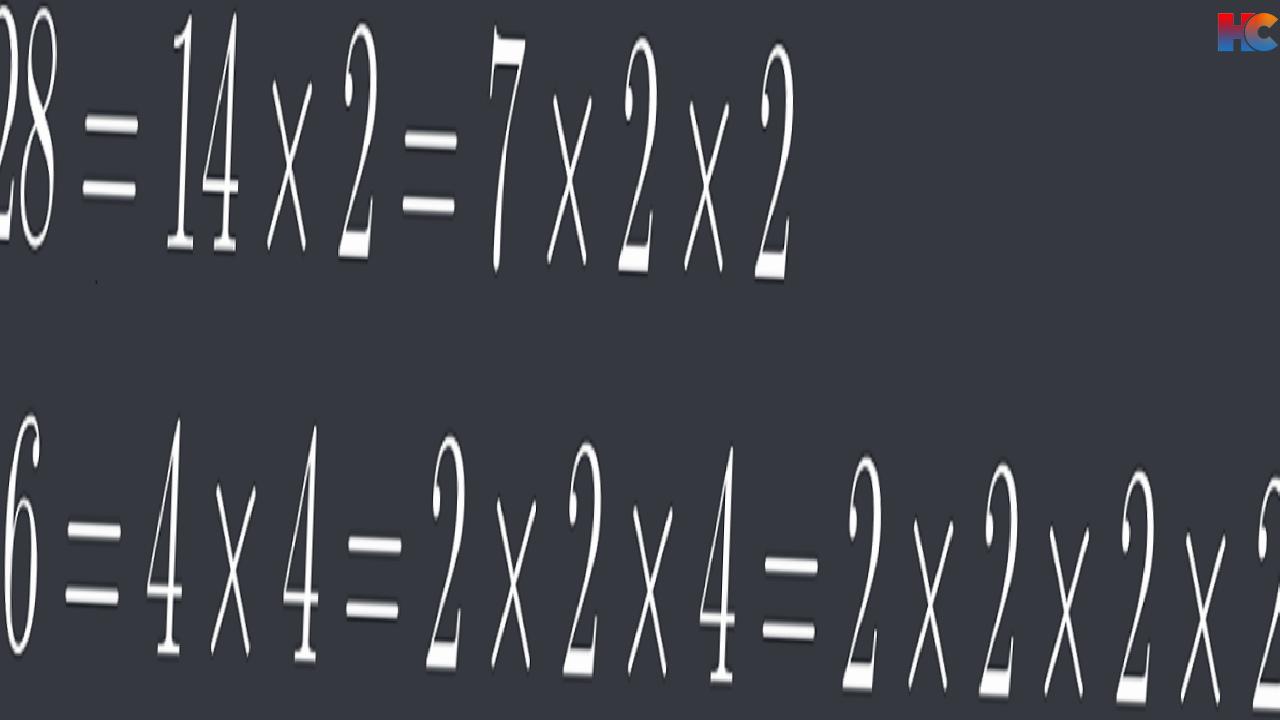
Yukarıdaki örneklerde verildiği gibi aynı şekilde 28 ve 16’yı asal çarpanlarına ayırıyoruz.
Adım 2#: Belirlenen sayıları üslü sayılar halinde düzenlemek
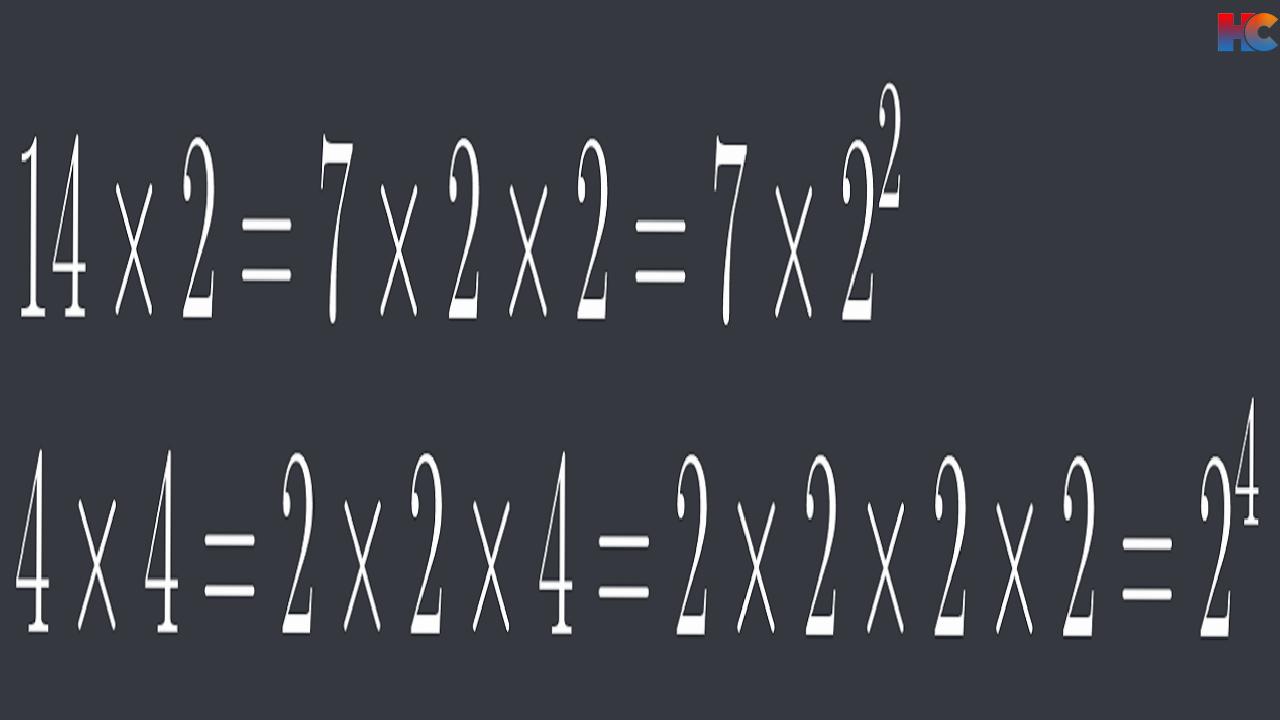
Asal çarpanlarına ayırdıktan sonra belirlediğimiz sayıları üstlü sayılar hailne getiriyoruz.
Adım 3#: Kuvveti en yüksek olanlar ile çarpmak
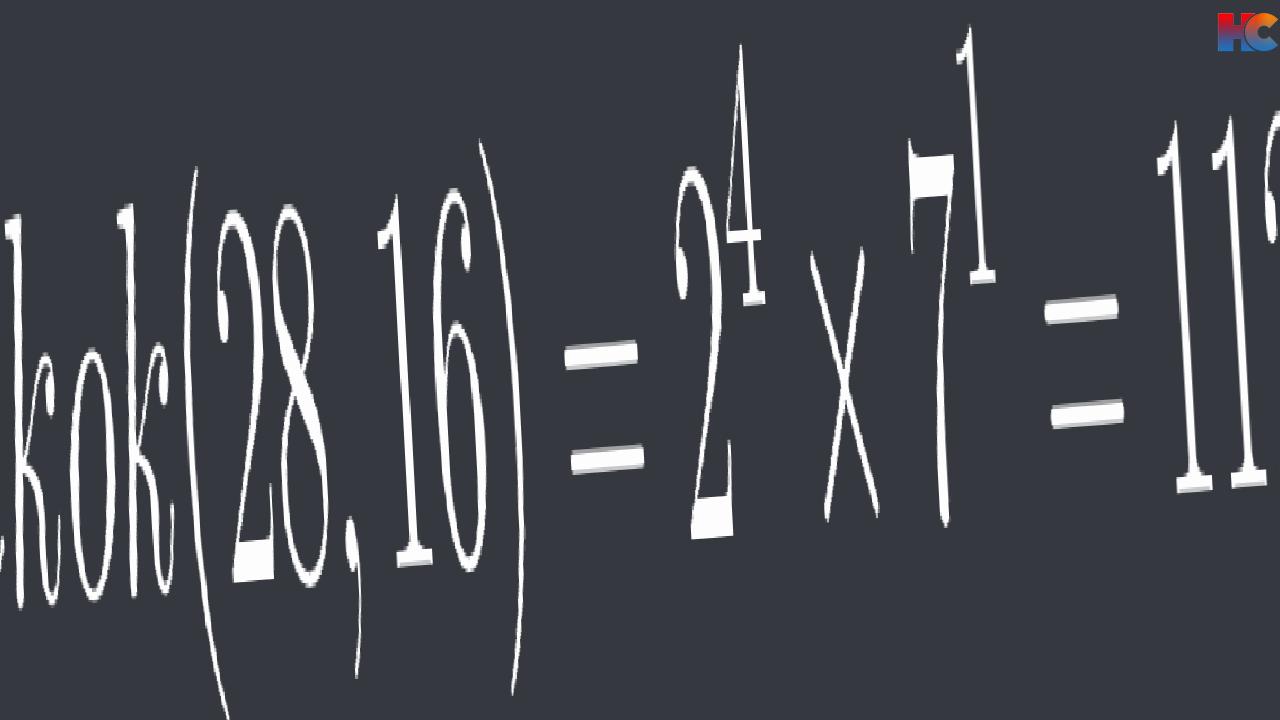
Buradaki çarpanlar arasında kuvveti en yüksek olanları alıp çarpacağız. Yani 7’nin kuvveti 1 olduğundan 7 üzeri 1, 2’nin en yüksek kuvveti 4 olduğundan 2 üzeri 4 ü çarpıma ekleyeceğiz. İşlemi yaptığımızda cevap 112 bulunuyor:
EBOB ve EKOK hesaplama araçları:

EBOB ve EKOK’un nasıl hesaplanacağını yukarıda belirttik. Ne kadar kendi elimizle yapacağımız yollar olsa da, bu hesaplamaları bizim yerimize yapan uygulamalar da mevcut. Bu uygulamalar genel anlamda kullanımı ücretsiz ve bir çoğuna internet üzerinden kolayca erişebiliyorsunuz. İnternet sitelerinin yanı sıra mobil cihazlarınızdan da EBOB ve EKOK hesaplayacak uygulamalara çok rahat bir şekilde erişebilirsiniz.
Andorid için EBOB ve EKOK hesaplama araçları:
İOS için EBOB ve EKOK hesaplama araçları:
iOS mağazasında bulabileceğiniz uygulamalar maalesef Android’deki kadar çeşitli değil ve uygulamanın kendisi paralı. Fakat yinede örnek olarak vermek istedik.





